数学
mod p^kにおける平方根
x2=a(modp)
の解がわかると
x^2 = a \pmod{p^2}
を解くことが出来たのでした。同じ考え方で任意のp^kについて次のようにして求めることが出来ます。
(x-\sqrt{a})^k
を計算して
\sqrt{a}の係数が\pmod{p^k}で1になるように逆数を乗じればokです。
\sqrt{a}の係数がpで割り切れてしまうとまずいのでそのことだけ証明しないといけませんが、結論だけから言うとその係数は
(2u)^{k-1}に\mod{p}で等しくなります。つまりu^2=a\pmod{p}としたとき
(u_{k}-v_{k}\sqrt{a}) =(u-\sqrt{a})^k
とすると
v_k=(2u)^{k-1}\pmod{p}
となります。よってv_kはpと互いに素で、逆数が存在することになり解を求めることが出来ます。
mod p^2における平方根
の解がわかると
x^2 = a \pmod{p^2}
を解くことができます。その手順について解説します。
x^2 = a \pmod{p}の解があるということは
x^2 - a = up
なるuがあるということです。左辺は次のように変形することができます。
(x-\sqrt{a})(x+\sqrt{a})=up
両辺を二乗すれば
(x-\sqrt{a})^2(x+\sqrt{a})^2=u^2p^2
これより
\begin{aligned} ((x^2+a)-2x\sqrt{a})((x^2+a)+2x\sqrt{a})=u^2p^2\\ \end{aligned}
を得るので2xで各係数を割れば
\begin{aligned} \left(\frac{x^2+a}{2x}-\sqrt{a}\right) \left(\frac{x^2+a}{2x}+\sqrt{a}\right)=\frac{u^2p^2}{4x^2}\\ \end{aligned}
となり\frac{x^2+a}{2x}が解になります。最後の2xで割るというところが微妙ですが、これはここからp^2での剰余を考えて演算をするということで解決できます。
例
8^2-7=3\cdot 19\\
が既知とします。
\begin{aligned} (8-\sqrt{7})(8+\sqrt{7})&=3\cdot 19\\ (71-16\sqrt{7})(71+16\sqrt{7})&=3^2\cdot 19^2\\ \end{aligned}
ここで
16 x = 1\ \pmod{19^2}
なる数を探します。すると158であることがわかるので左辺の各項に乗じて19^2での剰余を求めると
(27-\sqrt{7})(27+\sqrt{7})=0 \pmod{19^2}
を得ることができます。
注)
2xがpと互いに素であることが重要です。xはあきらかにpと素ですが2を乗じているのでpは奇素数でなければなりません。
mod Pにおける平方根 その3
8N+1の素数について、もう一つ別の考え方を解説します。多分Tonelli–Shanksのアルゴリズムと同じ考えに基づくものと思われます。
p-1=2^s t(ただしtは奇数)とおきます。すると任意のxに対して
(x^t)^{2^s} = 1
ですからx^tは1の2^t乗根です。
例えば97を考えると
96 = 2^5\cdot 3
ですから x^3は1の32乗根です。一般的に1の32乗根は32個あり、そのうち16個が32乗してはじめて1になる数です。ある数\omegaが32乗して初めて1になる数とすれば
\omega^3, \omega^5, \cdots, \omega^31もまた32乗根してはじめて1になる数です。よって1つそのような数を見つければ他の数は自然と見つかることになります。
(余談ながらその逆数\omega^{-1}, \omega^{-3},\cdots, \omega^{-31}も然りです)
\omegaを32乗して初めて1になる数(例えば42)としてその数を2乗、4乗としてこれを木の形にしてみます。(下図参照)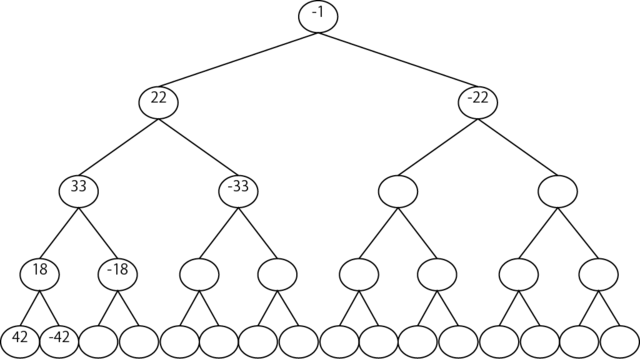
空白になっているところにも2の冪乗根があるはずですがそれは何かわからないので空欄にしておきます。また平方根についてはaが平方根の1つなら-aもまた平方根ですので剰余を0から95ではなく-48から47までの間になるように書いています。木の葉のほうから辿れば
42 → 18 → 33 → 22 → -1
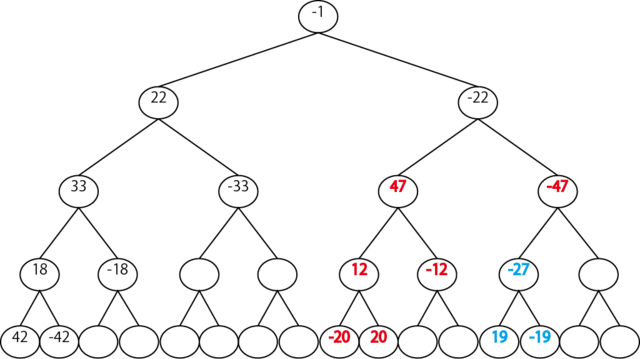
です。この中にa^3があれば答えは簡単です。例えばaが47とすれば、a^3=33ですから、1つ下の18を使って
a^3 = 33 = 18^2
これより両辺にaをかけて
a^4 = 18^2a
を得て
(a^2 18^{-1})^2 = a
が答えになります。18の逆数 (18 x =1なる数)が出てきますがこれは普通に求めてもいいし、そもそも18^{16-1}=27が逆数なのでそれを利用しても簡単に求まります。
答えとしては-12が得られます。実際-12^2=47です。
そうではない場合(例えば11)を探す場合は次のようにします。11^3=-27です。-27を冪冪で累乗していくと
\begin{eqnarray} (-27)^2 = -47\\ (-47)^2 = -22 \end{eqnarray}
となり、ここで-22が出ます。-22はツリーのルートのすぐ右側にあるので、この数はツリーの右側にあることがわかります。ところで\omegaですが次のような性質を持っています。
- \omega^2を乗ずると2段目のノードに対して左右に移動する
- \omega^4を乗ずると3段目のノードに対して左右に移動する
- \cdots
このルートの中に求めるノードがあればそれが答えです。残念ながら今回もみつからないので\omega^4を乗じます。そうすると-27が無事見つかりました。これから答えが求まります。
最後に32乗してはじめて1になる数の見つけかたですが、これは平方非剰余な数を3乗すれば求めるものになります。平方非剰余な数は全体の半数ですからランダムに選んで(p-1)/2乗して判定することができます。
この方法は運が悪いと沢山計算をする必要がありますが木の高さは sですから最悪でもs^2くらいのオーダーの計算量になります。
一方葉は2^sのオーダでこれを全部計算するのはsが大きくなるととんでもない数になります。sが小さいときは非効率ですが大きくなるにつれて優位性が増すと思われます。
mod Pにおける平方根 その2
a^n = \pm a (ただしnは偶数)
例えば有理数においても2の平方根は存在しませんが、仮にそれを\sqrt{2}と書くとすれば
x+y\sqrt{2}
という数の集合を考えることができてその集合に対して加減乗除が定義できます。例えば上記の数は二乗することが可能で二乗した結果は
(x^2+2y^2 )+ (2xy)\sqrt{2}
であってその結果もまた x + y\sqrt{2}の形に書けることがわかります。つまりx+y\sqrt{2}の形の集合を考えれば全ての加減乗除はその内部で閉じておりまた完結していることになります。
F_qもそれと同じ原理を用います。F_pから平方非剰余の数をT1つ選びその平方根があると仮定してそれを\sqrt{T}と表すことにし、この数をF_pに追加します。この集合に対して加減乗除が成立するためには
x+y\sqrt{T} と表すことができる数全て集めれば証明は割愛しますが十分で実際演算が閉じてうまく定義できることがわかります。xの選び方はp通りyの選び方はp通りですからこの体はp^2個の元からなることになります。このq=p^2とするとこの集合に対してもフェルマーの小定理が存在し
x^q=x
が成立することが知られています。つまりF_qではq乗すると元に戻ります。ところでF_pでは
x^p=x
が成立しました。したがってF_qで任意の元をp乗すると、F_pに含まれる数はその位置を変えません(固定される)。しかしF_pに含まれない数はそうではなく、別な数に移動しますがその数は共役元になることが知られています。つまり
(x+y\sqrt{T})^p = (x-y\sqrt{T})
です。となればF_qでは任意の元をp+1乗すると
(x+y\sqrt{T})^{p+1} = (x+y\sqrt{T})(x-y\sqrt{T}) = x^2 -y^2 T
となりその数がなんでありF_pに属することになります。今
x^2 -y^2 T=a
となるようにうまくx,yを選ぶことができればp+1は奇数ですから
(x+y\sqrt{T})^\frac{p+1}{2}
がその平方根になります。仮にyを1とすれば
T= x^2 -a
よってこのTが平方非剰余であるものを選んでその\frac{p+1}{2}乗を計算すればそれが答えになります。なお計算上はxとyだけが重要で\sqrt{T}が何ものであるかとは気にする必要がなく、x, yのペアでのみ演算をしTは二乗したらTとなる数とゆるく考えておけば問題ありません。つまり単純に無理数の\sqrt{T}と考えても問題ないということになります。
例)
p=41とし8の平方根を考えます。5^2-8=17は非平方剰余です。よってF_{1681}で考えることにより
(5+\sqrt{17})^{21}
が答えになります。
実際計算をしてみると
\begin{eqnarray} (5+\sqrt{17})^2=(1+10\sqrt{17})\\ (5+\sqrt{17})^4=(20+20\sqrt{17})\\ (5+\sqrt{17})^8=(25+21\sqrt{17})\\ (5+\sqrt{17})^{16}=(4+25\sqrt{17}) \end{eqnarray}
ですので
(5+\sqrt{17})^{16}(5+\sqrt{17})^{4}(5+\sqrt{17})^{1} =34
となります。
数が膨れあがらないのはその都度41で係数の剰余を取っているからです。また21回掛け合わせる必要はなく21は16+4+1ですから16乗、4乗、1乗したものを掛け合わせれば十分です。
余談)
F_pのような体を有限体(要素の数が有限なので)と言いますがその要素の数(位数とよぶ)は必ずpの冪であり、またpの冪の有限体は必ず存在することがわかっています。
mod Pにおける平方根
を求めるアルゴリズムとその原理の紹介です。アルゴリズムについては
mod pでの平方根
に書いてあるものと基本的に同じです。
任意の素数pに対して
a^{\frac{p-1}{2}} = \pm 1\pmod p
が成立しその符号はaが平方剰余かどうかで決まります。今回二乗してaになる数を探すのでaは必ず平方剰余です。つまり上式の値は1です。この式の両辺にさらにaを乗ずると
a^{\frac{p+1}{2}} = a\pmod p
よって\frac{p+1}{2}が偶数なら
(a^{\frac{p+1}{4}})^2 = a\pmod p
よって
a^{\frac{p+1}{4}}
が解になります。これはpが4N+3型の素数のときに使えます。簡単ですね。
そうではないとき(つまりpが4N+1型の素数のとき)は次のように考えます。
a^{\frac{p-1}{4}}=\pm 1 \pmod{p}
です。ここから両辺にaを乗ずると
a^{\frac{p+3}{4}}=\pm a \pmod{p}
よってpが8N+5型の素数ならば
\pm (a^{\frac{p+3}{8}})^2= a \pmod{p}
符号が正の場合はa^{\frac{p+3}{8}}が解になります。
負の場合は4N+1型の素数は-1が平方剰余であるのであらかじめ-1の根号(x^2=-1となる数。仮にiと記述する)を求めておけば ia^{\frac{p+3}{8}}が解になります。
iは平方非剰余の数を(p-1)/4すれば見つかります。1\cdots p-1なる数のうち半数が平方剰余で半数が平方非剰余ですから2から順番に探索していけば高確率ですぐ見つかりますが8N+5型については2が常に平方非剰余ですので2^{(p-1)/4}をあらかじめ計算しておけば良いことになります。
最後に残ったケース、pが8N+1型の素数についてはちょっとややこしいので次のエントリーに書きます。
ピタゴラスの定理の証明
任意の正方形は5つの破片に切って分けて新しい二つの任意の正方形を作ることができるんですよね。その逆も然り。

有限体の既約多項式の個数を求める
pを素数とし、q=p^nとする。有限体F_p上の多項式X^q-Xはdをnの約数とするとd次の約数既約多項式全てを因子に持つ。
証明はそんなに難しくないのでまたの機会にでもここに書きます。とりあえず、例を上げます(例が多いブログなもので・・・)
例1)
F_2上のX^{4} - Xの因数分解を考えます。n=2です。よって1次式と2次式の分解できます。実際計算してみると
\begin{eqnarray*} X^{4} - X = X(X+1)(X^{2} + X + 1) \end{eqnarray*}
となります。この式はこれ以上分解するのは不可能です。
例2)
F_2上の X^{8} - Xの因数分解を考えます。n=3です。
この式は3の約数である1次と3次の既約多項式を因子に持ちます。実際計算してみると
\begin{eqnarray*} X^{8} - X &=& X(X-1)(X^6 + X^5 + \cdots + 1)\\ &=& X(X-1)(X^3 + X + 1)(X^3 + X^2 + 1) \end{eqnarray*}
例3)
F_2におけるX^{16} - Xの因数分解を考えます。n=4です。
よってnの約数である既約4次式、2次式、1次式を因子にもちます。実際計算してみると、
\begin{eqnarray*} X^{16} - X &=& X(X-1)(X^{2} + X + 1)(X^{12} + X^{11} + \cdots + 1)\\ &=& X(X-1)(X^{2} + X + 1)(X^4 +X +1)(X^4 +X^3 +1)(X^4 +X^3 +X^2 +X +1) \end{eqnarray*}
以上なんとなく感覚がつかめていただいたでしょうか?2の冪以外の例はまた別の機会にここに書きます。
さて、ここからF_qにおけるn次の既約多項式の個数を求めます。
X^q-Xにおいてn次の既約多項式の根を全て掛け合わせたものの次数を\nu(n)とします。先ほどの例で言えば
\begin{eqnarray*} \nu(1)&=& 2\\ \nu(2) &=& 2\\ \nu(3) &=& 6\\ \nu(4) &=& 12\\ \end{eqnarray*}
です。この先ですが
\begin{eqnarray*} \nu(5) &=& 30\\ \nu(6)&=& 54\\ \end{eqnarray*}
と続きます。
さて、F_qにはnの約数であるd次の既約多項式がすべて存在します。それらの次数を足し合わせれば当然qになります。よって、
\begin{eqnarray*} \sum_{d|n}{\nu(d)} = q = p^n \end{eqnarray*}
が成立します。ここからメビウスの反転公式を使って
\begin{eqnarray*} \nu(d) = \sum_{d|n}{\mu\left(\frac{n}{d}\right)p^d} \end{eqnarray*}
となります。\nu(d) / nがn次式の個数になるので
\begin{eqnarray*} \frac{1}{n}\sum_{d|n}{\mu\left(\frac{n}{d}\right)p^d} \end{eqnarray*}
が求める個数になります。
オイラーのφ関数
wikipediaより
オイラーのトーシェント関数(オイラーのトーシェントかんすう、英: Euler's totient function)は各正の整数 n に対して、1 から n までの自然数のうち n と互いに素なものの個数を φ(n) として与えることによって定まる数論的関数 φ である。慣例的に φ(n) と表記されるため、オイラーの φ 関数(ファイかんすう、phi function)とも呼ばれる。また、簡略的にオイラーの関数と呼ぶこともある。
計算方法概略
簡単にするためまずnの素因数分解をp_1 p_2 p_3 \cdots p_nとし因子に平方数を含まないとします。 (つまり素数 p_1, p_2, p_3, \cdotsの羃は1)
1からnのうちp_1の倍数の数が n / p_1個あり、 p_2の倍数が n / p_2あり……ということでこれらの数をnから引きます。しかし、これでは p_1 p_2など2つの素数の積の数を2回引いてしまうのでそれらを足します。しかし、これでは p_1 p_2 p_3のような3つの素数の積になってる数を足しすぎてしまうのでそれらをまた引きます……と考えていけば……
\begin{eqnarray} \phi(n) = n &-& (n / p_1 + n / p_2 + \cdots + n / p_n)\\ &+& (n / p_1p_2 + n / p_1p_3 + \cdots + n / p_{n-1}p_n)\\ &-& (n / p_1p_2p_3 + n / p_1p_2p_4 + \cdots + n / p_{n-2}p_{n-1}p_n)\\ &+& \cdots \end{eqnarray} この式の分母の素数の積はnの全ての約数を渡ることは明かです。nの約数dを素因数分解したとき、それが偶数個ならn/dを足し、奇数個ならn/dを引いていくという流れになります。なお、上記の式は以下のように書けます。 \begin{eqnarray} \phi(n) = n(1 - 1/p_1)(1 - 1/p_2)(1 - 1/p_3)\cdots(1 - 1/p_n) \end{eqnarray}例
\begin{eqnarray} \phi(30) &= 30 - (30 / 2 + 30 / 3 + 30 / 5) + (30 / 6) + (30 / 10) + (30 / 15) - 30 / 30 = 8 \end{eqnarray}平方数を含む場合ですが例えば 12のときを考えれば2の倍数を除去したときに12の因数である4の倍数は既に除去されています。つまり、平方因子をもつ約数は考慮しなくてもよいのです。(つまり、素因数が何種類あるか?が重要)これはそのまま一般に拡張出来ます。実際上記の式は nの素因数分解をp_1^{e_1} p_2^{e_2} p_3^{e_3} \cdots p_n^{e_n}と分解される場合でも成立します。
n = p_1^{e_1} p_2^{e_2} p_3^{e_3} \cdots p_n^{e_n}の素因数をそれぞれの項に配分していけば
\begin{eqnarray} \phi(n) &=& p_1^{e_1}p_2^{e_2}\cdots p_n^{e_n}(1 - 1/p_1)(1 - 1/p_2)(1 - 1/p_3)\cdots(1 - 1/p_n)\\ &=&(p_1^{e_1} - p_1^{e_1-1}) (p_2^{e_2} - p_2^{e_2-1})\cdots (p_n^{e_n} - p_n^{e_n-1}) \end{eqnarray}なお、上記の式はメビウス関数を使えば \begin{eqnarray} \phi(n) = \sum_{d|n}\mu({d}){\frac{n}{d}} \end{eqnarray} とも表わすことができます。メビウス関数\mu({n})は
- nが平方因数を含む場合は\mu({n})=0
- nが因数を偶数個含む場合は\mu({n})=1
- nが因数を奇数個含む場合は\mu({n})=-1
ここからメビウスの反転公式を使って
\begin{eqnarray} \sum_{d|n}\phi(d) = n \end{eqnarray} とか即座に得られるのがまた味わい深いですの。以上Mathjaxのリハビリでした
4n+1の素数を平方の和にする(その2)
相当前にエントリに書いた4n+1の素数を平方の和にするアルゴリズムですがガウス整数を使ったもっとスマートな解法を紹介します。
まず前回同様 pを4n+1の素数として A^2 + 1 = 0 (\mod p) なるAを求めます。
A^2 + 1 = k p です。
左辺はガウス整数を使うとさらに因数分解できて (A + i)(A - i) = k p となります。
ここでガウス整数は通常の整数と同様、素因数分解等素数の性質があることを踏まえて等式を見てみます。
pはあきらかにA+iおよびA-iを割きりません。ということはpはガウス整数の世界ではさらなる素数に分解できることを意味します。すなわち最大公約数(A+i, p)は1ではなく、x+iyの形をしたガウス整数となります。
(A+i, p) = x + iy ならば共役の関係から (A-i, p) = x - iyがまた成立します。 一方(x + iy)(x - iy)を考えるとこれは有理整数x^2+y^2となりこれはpを割り切らないといけませんが、 pは素数ですから結局これはpに等しくp = x^2 + y^2となります。
つまりpとA+iの最大公約数を求めればそこから解は自動的に求まることになります。
最大公約数はガウス整数の世界でもユークリッドの互除法で簡単に求めることができます。
例として、素数p=120710677を二つの和にしてみます
46505545^2 + 1^2 = 17916938 \times 120710677
ですから最初は46505545+iと120710677の最大公約数を求めればよいことになります。
A_0 = 46505545+i\\ B_0 = 120710677 とします。
ノルムを比較すると|A_0| < |B_0|で A_0 = 3 * |B_0| + ... ですから最初の計算では A_1 = A_0, B_1 = B_0 - 3A_0とすればよいことがわかります。 実際計算してみると A_1 = 46505545+i\\ B_1 = -18805958-3i となります。以下同様にして計算していくと
\begin{align} A_2&=&8893629-5i, B_2&=&-18805958-3i\\ A_3&=&8893629-5i, B_3&=&-1018700-13i\\ A_4&=&-274671-122i, B_4&=&-1018700-13i\\ A_5&=&-274671-122i, B_5&=&79984+475i\\ A_6&=&-34719+1303i, B_6&=&79984+475i\\ A_7&=&-34719+1303i, B_7&=&10546+3081i \end{align} ここでB_7が求める答えになります。実際 10546^2+3081^2 = 120710677 です
注意
ユークリッドの互除法ではノルムの大きいほうをノルムの小さいほうで割ってその余りに置き換えるという手順を踏むのですが、それは以下のようにして求めます。
a+ibをc+idで割る場合は \frac{a+ib}{c+id} = \frac{(a+ib)(c-id)}{c^2+d^2} = \frac{ac+bd}{c^2+d^2} + \frac{bc-ad}{c^2+d^2}i ここで、有理数 \frac{ac+bd}{c^2+d^2}, \frac{bc-ad}{c^2+d^2} に最も近い整数をn, mとすれば (a+ib) = (n+im)(c+id) + (r+is) と書いたときに、r+isのノルムはc+idより小さくなります。よってr+isを余りとみなして計算を進めていくことができます。
別の考察
この例では(A+i, p)を考えましたが、(A+i, k)を考えても同様に計算をすることができることがわかります。
この場合最大公約数を求めなくても以下のように計算をすることができます。a^2 + b^2 = 0 (\mod k) であることを考えると a' = a(\mod k), b' = b(\mod k)とおけば a'^2 + b'^2 = 0 (\mod k) もまた成立します。つまりa'^2 + b'^2はkを割りきります。つまり \frac{(a+ib)(a-ib)}{(a'+ib')(a'-ib')} = \frac{k}{a'^2 + b'^2}p = k'p が成立します。右辺は整数ですから左辺は共役なガウス整数の積にならなければなりません。 よって \frac{a+ib}{a'+ib'}または\frac{a+ib}{a'-ib'} のどちらかがガウス整数になります。ここで \begin{align} -k/2 &<& a' &<& k/2\\ -k/2 &<& b' &<& k/2 \end{align} なるように a', b'を選べば kより小さい k'が見つかることになります。 この手順を繰替えせば kより始めていつかは1になるので求める解を見付けることができます。
これが前回解説したアルゴリズムと同じものになります。
さらりと流した部分の補足
有理整数がガウス整数の積で表わされる必要条件は共役の因子を含むことである。
ガウス整数をそれぞれ a+ibとc+idとする。c\ne 0, d\ne 0, (a,b)=1, (c,d)=1と仮定して問題ない。 なぜならもし(a,b)=k > 1ならばa' = a/k, b' = b/kとして k(a' + ib')(c+id)を考えればよいからである。 (a+ib)(c+id) = (ac-bd) + i(ad+bc) が有理整数なのだからad+bc=0すなわち ad=-bcが成立する。 よって、aとbと互いに素だからcがdを割り切りかつdがcを割きらなければならないが、 これは c=dまたはc=-dを意味する。c=dとすればa=-bでありc=-dとすれば a=bである。 いずれにしても共役の因子を含まなくてはならない。
有理整数が共役の数の積で表わされているのなら、その数はガウス整数でなければならない。
a/bおよびc/dを考える。(a,b)=1, (c,d)=1と仮定して問題ない (\frac{a}{b}+i\frac{c}{d})(\frac{a}{b}-i\frac{c}{d}) = \frac{a^2c^2}{b^2d^2} から b^2d^2 = 1 これはb=\pm 1, d=\pm 1を意味する。
x^2 = a (mod P)を効率よく解く
有限体Fp上で
x^2 = a
を解くことを考えます。根があるかないかは平方剰余の相互法則
x^2 = aが Fp根を持つ <=> (a/p) = 1 (ルジャンドルの記号) <=> a^(p-1)/2 = 1
で簡単に分かるのですが具体的にxが何であるかを求めるにはどうしたらよいのでしょうか?
Fpは有限群なので全ての元について根かどうかを解けばよいのですが、この手法はpが大きくなると破綻するのは自明です。そこで、ここでは別のアプローチを紹介します。
以下 aはFpで平方剰余であると仮定しておきます。また実数の世界にあやかって、x^2=aなるxを√aと表すことにします。(このようなxは2つ存在しもう一方は-√aです)。
pが4n+3型の素数のとき
pが4n+3ならば話は簡単です。
aは平方剰余なので
a^(p-1)/2 = 1
です。この両辺にaをさらに掛ければ
a^(p+1)/2 = a
となります。しかし、(p+1)/2は偶数ですから
a^(p+1)/4 = √a
ゆえに a^(p+1)/4が根(のうちの1つ)です。
pが4n+1型の素数のとき
この場合(p-1)/2が偶数のため(p+1)/2が奇数となり上の手法は使うことができません。ならば(p-1)が奇数になるまで 2で割るのはどうでしょうか?すなわち
p-1 = 2^k * s
とし、a^s乗を考えるのです。このa^s はあと2^k乗すれば 1になるのですから1の2^k乗根です。このa^sは原始的かどうか(すなわち 2^k乗根して始めて1になるかどうか)はわかりません。しかし仮に1つ原始2^k乗根を知っているとすれば全ての2^k乗根は
1, r, r^2, r^3, ..., r^(2^k-1)
とかけます。このようなrはこちらの手法で試行錯誤的に(だが簡単に)見つけることができます。さらに aは平方剰余だということがわかっているので実際は偶数番目だけのどれかであり、
a^s = r^2n
と書けます。このnが何かは今はわかりません。(この手法では最後までこのnが何かはわかりません)。しかし、nが何であるかわからなくても r^2n * r^2m=1となるようなmを見つけることができます。それには次の性質を利用します。
x, y が原始N乗根ならば x * y は原始N/2乗根である。
つまり原始128乗根どうしを掛け合わせると原始64乗根になるということです。ある数が原始何乗根かどうかはその数を自乗していき-1になる冪を調べればわかります。以下例で説明したほうがわかりやすいと思いますので例で解説します。
例
p=769 , a=8として x^2 = a を解くとします。p-1=768 = 3 * 2^8 ですからF769には原始256乗根が存在し、試行錯誤法で計算するとr=7であることがわかります。
a^3 = 8^3 = 512
です。512は
512^64 = -1
ですから、原始128乗根の1つ、すなわち
1, 7^2, 7^4, ... 7^254
のうちのどれかです。
そこで原始128乗根である 7^2 = 49 をかけることにより原始64乗根(もしくはそれ以上)にすることができます。実際かけてみると
8^3 * 7^2 = 480
となり480は
480^32 = -1
ですから、原始64乗根です。そこで原始64乗根である 7^4 を両辺にかけます
8^3 * 7^2 * 7^4 = 518
518は同様の計算で原始32乗根ですから 7^8を両辺にかけます。
8^3 * 7^2 * 7^4 * 7^8 = 729
729は原始8乗根です(原始16乗根をすっとばして2段階あがった)ので、両辺に7^32をかけます
8^3 * 7^2 * 7^4 * 7^8 * 7^32 = 707
707は原始4乗根ですから両辺に7^64をかけます。
8^3 * 7^2 * 7^4 * 7^8 * 7^32 * 7^64 = 1
ここで始めて1となりました。両辺に8をかけると
8 * 8^3 * 7^2 * 7^4 * 7^8 * 7^32 * 7^64 = 8
となり左辺の指数はすべて偶数です。故に
8^2 * 7 * 7^2 * 7^4 * 7^16 * 7^32 = √8
となります。左辺を計算してみると503になります。たしかに
503^2 = 8
です。