円分多項式その２

2007年02月19日(月)

その後いろいろがんばって結果、解が計算できました。。ヒントはWikipedia。

このエントリからの続きです。

最初にη1、η2を求めて方程式をつくりかえましたが、この段階で（有理数および√-7を含む数）が演算で作られる数が表現可能です。（こういう集合を体という）

この体をQ（√-7）とおきます。この体では

x^6+x^5+x^4+x^3+x^2+x+1 = (x^3 - η1x^2 + η2x - 1)(x^3 - η2x^2 + η1x - 1)　と因数分解できるのでした。

この次にやることは、ここにさらに別な数を加え、(x^3 - η1x^2 + η2x - 1)をさらに因数分解してやることです。そのために　a^3∈Q(√-7)でかつ、それ自身はQ(√-7)には含まれていない数を探します。これは以下のようにして求められます。

1の3乗根をωとしたとき、X、Y、Zを次のように置きます。

X = ξ^1+ ξ^2+ ξ^4 = η1 = 　(-1+√-7)/2

Y = ξ^1+ω ξ^2+ω^2 ξ^4

Z = ξ^1+ ω^2ξ^2+ ωξ^4

すると、

ξ=(X+Y+Z)/3

です。ところで、実際に計算してみると、

Y^3 +Z^3 = 14 - √-7

Y^3 Z^3 = -7√-7

となるので、Y^3, Z^3は

x^2-(14-√-7)x-7√-7

の解。これを解くと

(14-√-7±3√21)/2

これでX,Y,Zが全部求まるからξが計算できます。実際に計算すると、

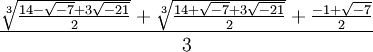
３乗根があるので、ここでうまく根を１つ選ばないと正しい解になりませんけど。これが１の7乗根（7乗すると１になる数）の１つとなります。

Googleで計算させるとこうなります。

あとは、ξ^2 ξ^3 ξ^4 ξ^5 ξ^6 も解だからこれで全部求めたことになります。

元祖ワシ的日記

円分多項式その２

2007年02月19日(月)

関連